令和3年2月期の過去問のうち、知っていればすぐに解ける計算問題をピックアップして解説していきます。
今回は令和3年2月期 工学A(17)を解説していきます。
令和3年2月期の過去問および解答は下記からダウンロード可能です。
問題【令和3年2月期 工学A(17)】

ヒント
下記の公式を用いて計算します。
<アンテナの利得>
$$G=\frac{4\pi A}{\lambda^2}\eta$$
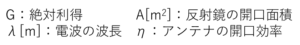
<波長>
$$波長=\frac{光速[m/s]}{周波数[Hz]}$$
解答
まずは波長を求めていきます
上記ヒントに記載した波長の公式から
$$\lambda=\frac{光速[m/s]}{周波数[Hz]}$$
光速および今回の周波数15[GHz]を代入すると
$$\begin{eqnarray}\lambda&=&\frac{3×10^8}{15×10^9}\\&=&\frac{1}{5}×10^{-1}\\&=&2×10^{-2} ①\end{eqnarray} $$
続いて絶対利得Gの値を真数に戻していきます
$$\begin{eqnarray}43&=&10\log_{10}G\\4.3&=&\log_{10}G\end{eqnarray}$$
ここで4.3を分解してGを求めていきます
$$\begin{eqnarray}4.3&=&4+0.3\\&=&log_{10}10^4+log_{10}2\\&=&log_{10}(2×10^4)\end{eqnarray}$$
上記により
$$G=2×10^4 ②$$
続いてアンテナの開口効率を求めていきます
$$G=\frac{4\pi A}{\lambda^2}\eta$$
こちらに①②で求めた
$$\lambda=2×10^{-2}$$
$$G=2×10^4$$
と問題文から
$$A=1.0$$
を代入して
$$\begin{eqnarray}2×10^4&=&\frac{4\pi×1.0}{4×10^{-4}}\eta\\\eta&=&\frac{2}{\pi}\\&=&0.636942\end{eqnarray}$$
よって答えは【4】の64%となります

こちらの問題は公式を覚えるのが非常に大変な問題です
私は公式をひたすら頭に叩き込んで、試験が始まったタイミングで覚えているうちに公式ありきの計算問題を真っ先に解いていました。
公式さえ覚えられれば後は計算だけですので、しっかり正解したいですね
参考 公式のあるぱか流覚え方
こちらの非常に覚えにくい難解な公式
<アンテナの利得>
$$G=\frac{4\pi A}{\lambda^2}\eta$$
私は「外国人の名前」として覚えていました
$$ジー=\frac{シパイエ}{ラムラム}エータ$$

自分流の覚えやすい覚え方を見つけてみてください!
類題【令和3年2月期 工学B(17)】

令和3年 2月期の工学Bより、類題を求めてみましょう

周波数と開口面積の数値が異なっていますが、解き方は全く同じです!
答えは【2】の65%になります
※他の計算問題についても解説しております。下記をご参照願います。





コメント