第一級陸上特殊無線の「工学」の計算問題で必須な公式/知識をまとめていきます
計算問題の基礎
デシベル計算について
回路の電力比や電圧比を計算するための「デシベル dB」について、おさらいしましょう。
log公式の基礎知識
※ これ以降のlogはlog10を略したものになります。 ※
10log10=10dB
や
20log20=26dB
logがとっつきにくい理由の一つです。これらを理解しないとlog計算問題は解けません。
それほど重要な公式です。
ですが、デシベルは関係性さえ覚えてしまえばなんてことはありません。
dB計算は他人に説明できるレベルになるまで毎日学習しましょう。
電力と電圧の関係
- 電力=W(ワット)=10log =こちらをベースに計算を考える。
- 電圧=V(ボルト)=20log =電力で導いた真数・dB値に対し、計算を加えて算出する。
電力(W)をベースにした真数とdBの関連性
真数:400 = dB:26 だとすると以下の関連性がある。
| ① | 真数における0の数 | → | dBにおける十の位と百の位の値 |
| ② | 真数における4や2などの値 | → | dBにおける一の位の値 |
真数とdBの関連性
真数における4や2など等の値 と dBにおける一の位の値 は
以下の5種類だけを暗記すれば良い。
| 真数 | dBにおける一の位の値 | |
| 1 | = | 0 |
| 2 | = | 3 |
| 4 | = | 6 |
| 8 | = | 9 |
| 5 | = | 7 |
解説
※dBは 3,6,9 と3の倍数で増えていき、0と7がプラスで付く
※真数は 2、4、8 と2の倍数で増えていき、1と5がプラスで付く
※これ以外の数字は 一の位 にでません。
■■■ 注意事項 ■■■
平成26年6月午後_問17に「12dB」という値がでました。
それ以前では出題されたことのない値です。(一の位に「2」は真数のみだった)
今後も出題される可能性があるため基本のもの以外に
dbのパターン例の応用として覚えておきましょう。
真数とdBの関連性をゴロ合わせで覚える
なかなか覚えられないという方は、
試験が始まったらすぐに問題用紙に書いておくと忘れずに対応できます。

例題で関連性を確認(電力によるものだけを記載)
真数からdBに置き換える
| 真数 | dB | 解説 | ||
| 20 | = | 13 | → | 真数に0が1個あるので10dB、 真数の頭に2が使われているので3dB =13dB |
| 800 | = | 29 | → | 真数に0が2個あるので20dB、 真数の頭に8が使われているので9dB =29dB |
| 5000 | = | 37 | → | 真数に0が3個あるので30dB、 真数の頭に5が使われているので7dB =37dB |
| 2000 | = | 33 | → | 真数に0が3個あるので30dB、 真数の頭に2が使われているので3dB =33dB |
| 4000000 | = | 66 | → | 真数に0が6個あるので60dB、真数の頭に4が使われているので6dB =66dB |
| 8 | = | 9 | → | 真数に0がないので0dB、真数の頭に8が使われているので9dB =9dB |
| 400 | = | 26 | → | 真数に0が2個あるので20dB、真数の頭に4が使われているので6dB =26dB |
dBから真数を導く方法
dBから真数に置き換える
| dB | 真数 | 解説 | ||
| 13 | = | 20 | → | dBの一の位が3なので真数の頭が2, dBの十の位が1なので0が1個 = 20 |
| 29 | = | 800 | → | dBの一の位が9なので真数の頭が8, dBの十の位が2なので0が2個 = 800 |
| 37 | = | 5000 | → | dBの一の位が7なので真数の頭が5, dBの十の位が3なので0が3個 = 5000 |
| 33 | = | 2000 | → | dBの一の位が3なので真数の頭が2, dBの十の位が3なので0が3個 = 2000 |
| 66 | = | 4000000 | → | dBの一の位が6なので真数の頭が4, dBの十の位が6なので0が6個 = 4000000 |
| 9 | = | 8 | → | dBの一の位が9なので真数の頭が8, dBの十の位が0なので0が0個 = 8 |
| 26 | = | 400 | → | dBの一の位が6なので真数の頭が4, dBの十の位が2なので0が2個 = 400 |
電圧 の求め方
電力値のdB変換をベースに考えていきます。
真数からdBに置き換える
| 真数 | dB | 解説 | ||
| 20 | = | 26 | → | 電力値でのdB変換が13dBだったので、2倍すると → 26dB |
| 800 | = | 58 | → | 電力値でのdB変換が29dBだったので、2倍すると → 58dB |
| 5000 | = | 74 | → | 電力値でのdB変換が37dBだったので、2倍すると → 74dB |
| 2000 | = | 66 | → | 電力値でのdB変換が33dBだったので、2倍すると → 66dB |
逆のパターンについても下記に記載します。
dBから真数に置き換える
| dB | 真数 | 解説 | ||
| 26 | = | 20 | → | dbの値を2で割ると13dBとなる、これを電力の求め方で計算すると → 20 |
| 58 | = | 800 | → | dbの値を2で割ると29dBとなる、これを電力の求め方で計算すると → 800 |
| 60 | = | 1000 | → | dbの値を2で割ると30dBとなる、これを電力の求め方で計算すると → 1000 |
| 66 | = | 2000 | → | dbの値を2で割ると33dBとなる、これを電力の求め方で計算すると → 2000 |
応用編
以下の12dB~24dBまでの真数変換は覚えておきましょう。
| dB | 真数 | 解説 (元dBを分解し、それぞれを真数に置換え乗算して値を求めています) | ||
| 3 | = | 2 | → | 3dB = 2倍 |
| 6 | = | 4 | → | 6dB = (3dB + 3dB) = (2 * 2) = 4倍 |
| 9 | = | 8 | → | 9dB = (3dB + 3dB + 3dB) = (2 * 2 * 2) = 8倍 |
| 12 | = | 16 | → | 12dB = (6dB + 6dB) = (4 * 4) = 約16倍[15.84倍] |
| 15 | = | 32 | → | 15dB = (9dB + 6dB) = (8 * 4) = 約32倍[31.62倍] |
| 18 | = | 64 | → | 18dB = (9dB + 9dB) = (8 * 8) = 約64倍[63.09倍]) |
| 21 | = | 128 | → | 21dB = (9dB + 9dB + 3dB) = (8 * 8 * 2) = 約128倍[125.89倍]) |
| 24 | = | 256 | → | 24dB = (9dB + 9dB + 6dB) = (8 * 8 * 4) = 約256倍[251.18倍]) |
光速の値
\begin{eqnarray}光速&=&3.0×10^8[m/s]\end{eqnarray}
- 光速は1秒間に3億[m] = 30万[km] 進みます
- 光速は1秒間に地球を7週半します。
- 月までの距離が38万kmなので、月まで電波を何の影響もなく飛ばすと、約1.27秒で届く
波長の値 (λ=ラムダ の公式)
λ(波長) = 光速 / 周波数
- 例
- 周波数5[GHz]の場合 → λ = 3×10^8÷5×10^9 → 3/50 = 0.06(m)
- 周波数6[MHz]の場合 → λ = 3×10^8÷6×10^6 → 300/6 = 50(m)
波長と周波数の仕組み
波長が”短く”なると、周波数は”大きく”なる。
波長が”長く”なると、周波数は”小さく”なる。
なぜ?
公式 「 波長 = 光速 / 周波数 」 より
周波数は分母であり、反比例するからである。
※分子の光速は 3.0×10^8 [m/s]で固定である。
数値を入れて考える。
A : 周波数が800MHzの場合 = 3×10^8÷800×10^6 = 0.375(m)
B : 周波数が6GHzの場合 = 3×10^8÷6×10^9 = 0.05(m)
C : 周波数が12GHzの場合 = 3×10^8÷12×10^9 = 0.025(m)
上記よりAが一番波長が長く、Cが一番波長が短いことがわかる。
このことから波長が短いほど、周波数は大きく(高く)なるので
フェージングや大気の影響を受けやすくなってしまう。
掛け算と割り算の関係
- 速度 × 時間 = 距離
- 距離 ÷ 速度 = 時間
- 距離 ÷ 時間 = 速度
覚えるべき単位
- K = キロ = 10^3 = 1,000
- M = メガ = 10^6 = 1,000,000
- G = ギガ = 10^9 = 1,000,000,000
- C = センチ = 10^-2 = 0.01
- m = ミリ = 10^-3 = 0.001
- μ = マイクロ = 10^-6 = 0.000001
単位の仕組み
- 10GHzから1MHzまで
- 10000000kHz = 10000MHz = 10GHz
- 1000000kHz = 1000MHz = 1GHz
- 100000kHz = 100MHz = 0.1GHz
- 10000kHz = 10MHz = 0.01GHz
- 1000kHz = 1MHz = 0.001GHz
- 1MHzから1Hzまで
- 1000000Hz = 1000kHz = 1MHz
- 100000Hz = 100kHz = 0.1MHz
- 10000Hz = 10kHz = 0.01MHz
- 1000Hz = 1kHz = 0.001MHz
- 100Hz = 0.1kHz = 0.0001MHz
- 10Hz = 0.01kHz = 0.00001MHz
- 1Hz = 0.001kHz = 0.000001MHz
- 1mから0.01mmまで
- 1000mm = 100cm = 1m
- 100mm = 10cm = 0.1m
- 10mm = 1cm = 0.01m
- 1mm = 0.1cm = 0.001m
- 0.1mm = 0.01cm = 0.0001m
- 0.01mm = 0.001cm = 0.00001m
ルート
- 送受信間の見通し距離 の計算で使用します
- √ 9 = 3
- √16 = 4
- √25 = 5
- √36 = 6
- √49 = 7
- √64 = 8
- 自由空間における電界強度 の計算で使用します
- √400 = 20
- √900 = 30
- √1600 = 40
- √2500 = 50
- √3600 = 60
【周波数】【波長】【周期】【振幅】とは何か(電磁波の基礎知識)
- 電磁波は電界と磁界の強さが周期的に変化する波です。
周期的に変化する様子を示すために変化の回数や変化の大きさ等についての用語があります。 - 周波数とは”1秒間に繰り返す変化(波)の回数”のことを示し単位はヘルツ[Hz]で表されます。
- 振幅は”波の高さ”を表します。単位は対象とするものによって異なりますが電圧や電流で表されるため、電圧の場合V(ボルト)はまたは電流の場合A(アンペア)を使用するのが一般的です。
- 波長とは”光速を周波数で割ったもの”で、(1回の変化が進む距離「1波長」で、波の山から山または谷から谷までの距離)単位はメートル[m]で表されます。
- 周期とは”1波長(サイクル)を進むのに要する時間”のことを示し、単位は時間[秒]です。

暗記必須な公式集
半波長ダイポールアンテナ※令和3年6月期出題
半波長ダイポールアンテナの実効長le[m]は下記の式で求められます。
\begin{eqnarray}l_{e}&=&\frac{\lambda}{\pi}\end{eqnarray}
また、波長λ[m]と周波数f[Hz]、光速[m/s]には下記の関係があります。
\begin{eqnarray} c&=&f \lambda\end{eqnarray}
分流器 ※令和3年6月期出題
下記の図のように、電流計に並列に接続した抵抗Rsを分流器といいます。

元々の電流計の測定範囲を、m倍に拡大するためには、 $$\begin{eqnarray}R_{s}&=&\frac{r_a}{m-1}\end{eqnarray}$$
の抵抗を並列に接続します。
パルスレーダー※令和3年10月期出題
電波の伝搬速度は光速と等しいため、3.0×108 [m/s]
$$距離=速さ×時間$$
の公式を用います。
電波の伝搬速度は光速と等しく、そして「パルス波が発射されてから、物標による反射波が受信されるまでの時間」は「往復分の時間」となります。

ケアレスミスに注意です!
有能電力※令和3年10月期出題
内部抵抗r、電圧Vの電圧源に、負荷抵抗Rが直列で接続されたような回路の場合、
負荷抵抗Rでの電力が最大となるのは、r=Rのとき となります。

上記のことを「供給電力最大の法則」といいます
また、その時の電力Pmaxを最大有能電力や最大電力といい、下記で求めることができます。
$$\begin{eqnarray}P_{max}&=&\frac{V^2}{4r}\end{eqnarray}$$
標本化※令和1年10月期出題
周波数帯域(アナログ) 15kHz → 標本化(デジタル) 30kHz → 周波数帯域(アナログ) 15kHz
と、なります。
最高周波数の2倍が標本化周波数
と覚えておきましょう。
有効シンボル期間長※令和3年2月期出題
【有効シンボル期間長】=1÷【周波数】=【有効シンボル期間長
もしくは 「時間間隔」と「周波数」は反比例の関係 を覚えておきましょう。
アンテナ開口率※令和3年2月期出題
<アンテナの利得>
$$G=\frac{4\pi A}{\lambda^2}\eta$$
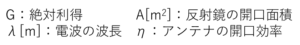
<波長>
$$波長=\frac{光速[m/s]}{周波数[Hz]}$$
電圧増幅度※令和2年2月期出題
負帰還増幅回路の利得(増幅率)の公式は下記で示すことができます。
$$\begin{eqnarray}\frac{V_out}{V_in}&=&\frac{A}{1+A\beta}\end{eqnarray}$$
オペアンプ(反転増幅回路)※令和3年6月出題
反転増幅器があります。

反転増幅器では、入力電圧Vinと出力電圧Voutの間に、下記の関係が成り立ちます。
\begin{eqnarray} V_{in}&=& \frac{R_2}{R_1}V_{out}\end{eqnarray}
つまり、抵抗R1と抵抗R2の比で電圧増幅度が決まります。
受信機の雑音指数
受信機の雑音指数(NF) = 1 + ( 等価雑音温度[K] / 周囲温度[℃] )
※周囲温度に「273」を足すのを忘れずに行いましょう。
マイクロ波回線の自由空間伝搬損失
自由空間伝搬損失Γ0は下記式で求められます。
\begin{eqnarray} \gamma_0&=& (\frac{4\pi d}{\lambda})^2\end{eqnarray}
見通し距離と等価地球半径
互いが見通せる距離の範囲dは、下記の様に算出できることが知られています。
等価地球半径係数K=1のとき
\begin{eqnarray} d≃3.57(\sqrt{h_1}+\sqrt{h_2}) \end{eqnarray}
等価地球半径係数K=4/3のとき
\begin{eqnarray} d≃4.12 (\sqrt{h_1}+\sqrt{h_2}) \end{eqnarray}
方形導波管
| 1 | 遮断波長 | 長辺×2 |
|---|---|---|
| 2 | 遮断周波数 | 光速/(長辺×2) |
| ※ | 光速=3×10^8 | =300,000,000 (m/s) |
まとめ
必要に応じて順次更新していきます。













コメント